PCA

主成分分析

模型引出

• 在实际问题研究中,多变量问题是经常会遇到的.
  • 变量太多无疑会增加分析问题的难度与复杂性
  • 多个变量之间可能具有一定过的相关性
• 主成分分析法
  • 设法将原来的变量重新合成一组新的互相无关的几个综合变量
  • 根据实际需要从中可以取出几个较少的综合变量尽可能多地反映原来变量的信息
• 数据降维
  • 降维是将高维度的数据(指标太多)保留下一些最重要的一些特征,去除噪声和不重要的特征,从而实现提升数据处理速度的目的
  • 在实际生产和应用中,降维在一定的信息损失范围内可以为我们节约大量的时间和成本
  • 优点
    • 使得数据集更易使用
    • 除噪声
    • 降低算法的计算开销
    • 使得结果容易理解

模型原理

• 主成分分析原理

  • 对一个样本矩阵:换特征 减少特征
  • 将n维原始特征映射到k维上
    • 不是简单地去除n-k维特征
    • 重新构造出全新的k维正交特征,且新生成的k维数据尽可能多地包含原来n维数据的信息
  • 找到新的维度:保证数据间的方差够大

• 

• 
• 
• 

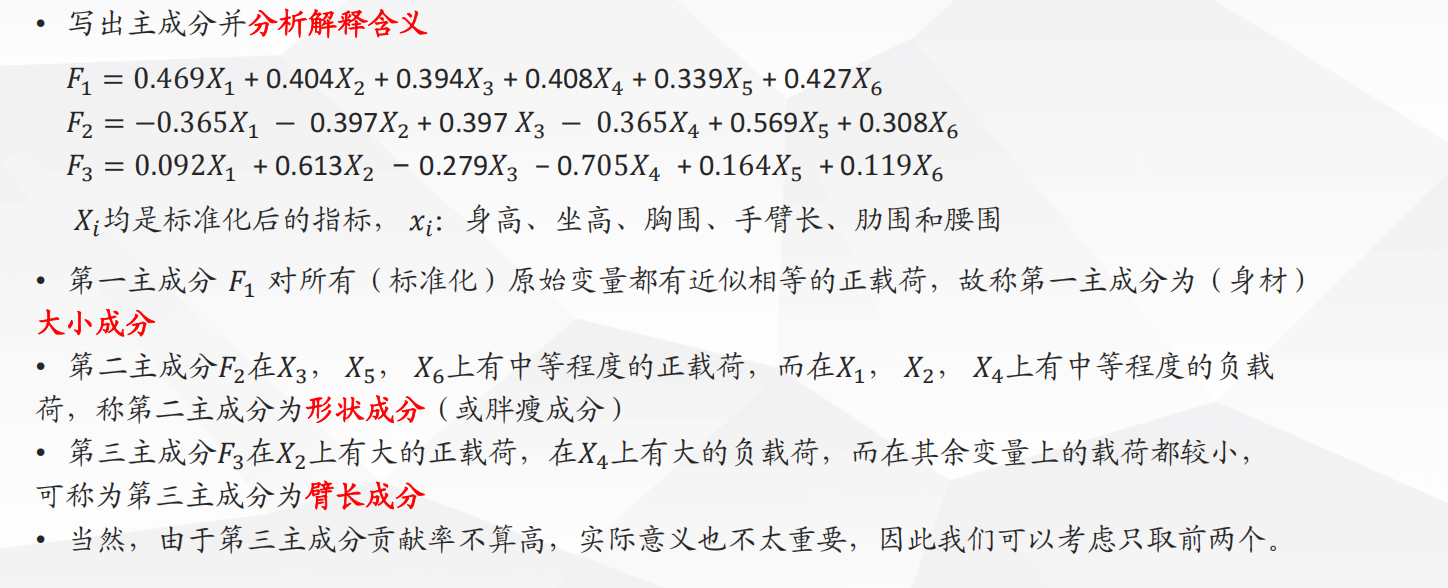
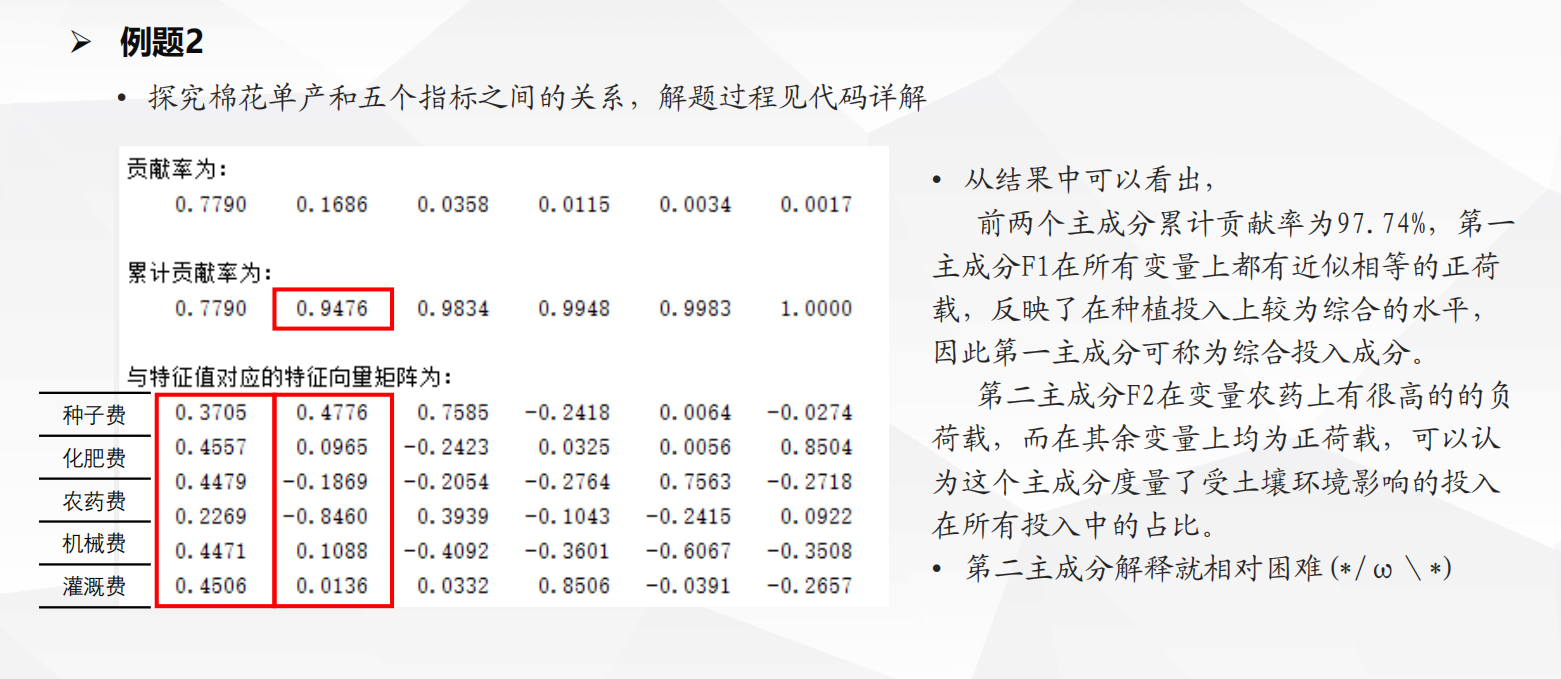
可以查一查相关领域的论文来看一看如何进行解释